N.S.E.A. Protector Scaling Page
The N.S.E.A. Protector is one of the newest sci-fi ships, from the sci-fi comedy (and part Star Trek spoof) Galaxy Quest, starring Tim Allen, Sigourney Weaver, and Alan Rickman. In the movie, it's a fictional ship from a 70s show that alien Thermians actually build (straight down to a plot device, the Chompers), and eventually is crewed by the actors who played in the show.
The size of the Protector will not be as easy to come by as the size of the Rodger Young. The Rodger Young had an easy measuring stick: an average human being. However, we never get such an opportunity in Galaxy Quest. The good news is that there IS a usable "measuring stick": a car during the crash landing of the Protector's detachable bridge module. Therefore, we will use that to determine the height, width, and length of the N.S.E.A. Protector.
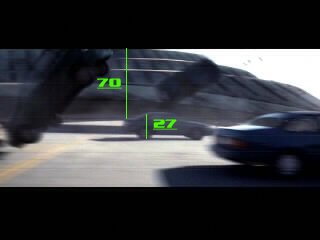
The car is 27 pixels high, while the bridge module is 70 pixels. Assuming a five foot height for the car, which converts into 1.5 meters, we can establish the bridge module as being 3.8 meters in height.
However, five feet for the car height is a pretty high estimate. A more realistic four feet, or 1.2 meters, indicates the bridge module is 3.1 meters.
Next, we have a side shot of the Protector leaving it's dock at the Thermian space station.

The bridge module is 15 pixels high. The Protector's height is 82 pixels. Therefore, with the 3.8 meter height for the bridge module from the five foot car estimate, we can establish the Protector as being 20.7 meters in height. Using the four foot car estimate, we get 16.9 meters for the height.
Now to determine the width. As it was only one movie, with very few actual shots of the Protector and even fewer scalable shots, I was unable to find a direct height-to-length shot, but did find height-to-width and width-to-length shots, so we'll do this the long way. :-)

Since the ship is slightly tilted, I applied Pythagorean Theorem. I did this by drawing a line across the width of the ship, then using it as the hypotenuse for a right triangle. After measuring the pixels of the other sides of the triangle, I applied the formula A^2+B^2=C^2, and came up with 228 pixels. The height of the ship is 57 pixels, the width is 228. Using the 20.7 meter number for height, the maximum width of the Protector turns out to be 82.8 meters. With the second, lower estimate based on the four foot height for the car, it comes out to be 67.6 meters.
Now comes the hard part. This following pic has a good width-to-length conversion, but both are at slanted angles, which means that BOTH had to be measured with Pathagaras Theorem.
First I did the known quantity: the width.

Once again I made a triangle with a right angle to apply the formula. With one side at 23 pixels and the other at 63, the total came out to be 67 pixels.
Next comes the length.

One side was 21 pixels, the other 76. Once the formula was applied, it came out to be just under 79 pixels.
It's pretty damned embarrassing, but while recalculating for the new four foot car height, I noticed that the length difference was way too high. I went back to my original calculations, and found I had plugged in the wrong pixel number for my original length calculations! So I corrected it, and the true length for both the numbers are as follows:
Assuming four foot height for car: 79.7 meters
Assuming five foot height for car: 97.6 meters
So, the Protector has the following dimensions by range:
| Height | 16.9-20.7 meters |
| Width/Wingspan | 67.6-82.8 meters |
| Overall Length | 79.9-97.6 meters |
That means it's not as long as the White Star from Babylon-5 or the Defiant from Star Trek: Deep Space Nine, but somewhat longer than the Millennium Falcon from Star Wars. In terms of size, the Protector is similar to the various attack submarines launched in the 1960s and onward (the Los Angeles-class, the most noticable part of the US Navy's attack submarine fleet, is 360 feet, or 109.73 meters), particularly the Skipjack, Permit, and Narwhal-class SSNs. Considering the maximum amount of crew we see and the shape of the primary hull, it's not too hard to see the Protector as a "submarine" of sorts.
Acknowledgements:
Brian Young, for showing me the secret to scaling (I still feel like an idiot for not realizing it sooner) and recommending Pythagorean Theorem in angled shots.
Julius Sykes, for giving me the corrected name for Pythagorean Theorem.